## Load the packages
library(ISLR)
library(FNN)Section 4 - Classification
Notes
Note that the material in these notes draws on past TF’s notes (Ibou Dieye, Laura Morris, Emily Mower, Amy Wickett), and the more thorough treatment of these topics in Introduction to Statistical Learning by Gareth James, Daniela Witten, Trevor Hastie and Robert Tibshirani.
Logistic Regression
Concept
Logistic regression is a parametric model that models the probability that \(Y\) belongs to a particular category. It is somewhat similar to linear regression, but the linear regression form of \(\beta_0+\beta_1 X_1 + \beta_2 X_2 + \dots\) undergoes a transformation that ensures the output will be bounded between 0 and 1 and can thus be interpreted as a probability.
\[\begin{equation} p(X) = \frac{e^{\beta_0+\beta_1 X}}{1 + e^{\beta_0 + \beta_1 X}} \end{equation}\]
Therefore, while linear regression is best suited for regression problems, logistic regression is best suited for classification problems. Note that logistic regression produces a probability of class membership that then needs to be transformed to 0 or 1 using a decision rule, such as if \(p(X)\geq 0.5\) then predict 1 otherwise predict 0.
Method
Logistic regression is estimated using Maximum Likelihood Estimation (MLE). MLE finds the values of \(\beta_0\), \(\beta_1\), etc. that maximize the probability of observing the observations in your training data given the values of the parameters \(\beta_0\), \(\beta_1\), etc. and the assumed functional form (e.g. see above).
Implementation and Considerations
When implementing logistic regression, the restrictions on the features are the same as for linear regression (e.g. no collinearity, number of features must be less than number of observations, etc.). The outcome should be a binary class membership. You can extend the logistic regression to cover a scenario with more than two classes, and this is called multinomial logistic regression, but we will not cover that in class.
When you run logistic regression, the prediction output is a continuous value that reflects the predicted probability that the observation belongs to class 1. Therefore, a decision rule is required to convert the predicted probability to a predicted class (0 or 1). If you care equally about wrongly predicting positive for a True Negative (e.g. predicting class 1 for someone who is actually in class 0) and predicting negative for a True Positive, then a good decision rule is if \(p(X)\geq 0.5\), predict 1 and otherwise predict 0. However, sometimes you care more about an error in one direction than the other. An example of this would be not wanting to offer a loan to someone who will default even if that means you deny more people who wouldn’t default. In that case, you might lower the threshold to 0.2 or some other value. We explore this more in the code.
Review of High-Level Concepts
Methods
At this point in the course, you have been introduced to three methods. The methods and their properties are summarized in the table below.When thinking about if a model is parametric or non-parametric, it can be helpful to think: Do I have a set of parameters that I can use to find the predicted value of any new observation? If yes, it’s parametric. When thinking about if a problem is a classification problem or a regression problem, it is helpful to think about the outcome in the training data. If the outcome is continuous, then it’s a regression problem. If the outcome is categorical, it’s a classification problem. The emphasis on the outcome in the training data is to avoid the confusion that arises when you look at prediction output. As we saw with logistic regression, even though it’s a classification problem, the output will be a probability (which is continuous and needs to be converted to 0 or 1 in order to measure performance).
Classification
Classification is really a two-step process. Usually, the model will predict something that looks like a probability that your observation belongs to each class. You then need to convert the probability to a class membership using a decision rule. A good general rule is: ``whichever class is assigned the highest probability is the predicted class.’’ However, when you have reason to prefer an error in one direction (e.g. predicting more people will default than actually will), you should change this threshold. Exactly which threshold is optimal will depend on domain knowledge and other factors (such as how costly defaults are or how profitable repaid loans are).
Discriminant Analysis
Concept
Recall that the Bayes’ Classifier is the unattainable gold standard classifier. It assumes knowledge of the true underlying distribution of the data, which you will not have in practice. Given features \(X\), it knows the true probability that \(Y\) belongs to each possible class. It predicts the most likely class, which is the best decision rule given the available features.
Linear Discriminant Analysis (LDA) approximates the Bayes’ Classifier, given the information available and the assumption that features are Normally (Gaussian) distributed within each class. The result is decision boundaries that are linear in the included features.
When there is one feature (predictor), LDA estimates class-specific means \(\hat{\mu}_k\) and a single variance \(\hat{\sigma}^2\) that is common to all classes. When there are multiple features, LDA estimates class-specific mean vectors \(\hat{\mu}_k\) and a single variance-covariance matrix \(\hat{\Sigma}\) that is assumed to be relevant to all classes. In both cases (one feature or many features), LDA also calculates the unconditional probability of belonging to each class \(\hat{\pi}_k\). LDA then takes these components (means, variance, and unconditional class probability) and calculates a discriminant function for each observation and each class. For each observation, the predicted class is determined by the largest discriminant.
Quadratic Discriminant Analysis (QDA) is conceptually similar, though instead of requiring all classes to share the same variance or variance-covariance matrix, it allows for class-specific variances. This has the effect of allowing non-linear decision boundaries. The drawback, though, is that allowing for class-specific variances (and especially class-specific variance-covariance matrices) increases the number of parameters to estimate, increasing the likelihood of overfitting.
Method
To estimate LDA or QDA, you estimate the feature means, feature variance(s), and unconditional (empirical) class probabilities for each class. Let \(k\) index the classes, then if there is only one feature, LDA calculates the following discriminant function for each observation for each class: \[\begin{equation}
\hat{\delta}_k(x) = x \cdot \frac{\hat{\mu}_k}{\hat{\sigma}^2}-\frac{\hat{\mu}_k^2}{2\hat{\sigma}^2}+\log(\hat{\pi}_k)
\end{equation}\] Where \(\hat{\pi}_k\) is the unconditional class probability, \(\hat{\mu}_k\) is the mean feature value for class \(k\), and \(\hat{\sigma}^2\) is the common feature variance. When \(p>1\) (e.g. there are multiple predictors), then we use \(\hat{\Sigma}\) to represent the common feature variance-covariance matrix, \(\hat{\mu}_k\) becomes a vector, and thus the LDA discriminant function becomes: \[\begin{equation}
\hat{\delta}_k(x) = x^T\hat{\Sigma}^{-1}\hat{\mu}_k-\frac{1}{2}\hat{\mu}_k^T\hat{\Sigma}^{-1}\hat{\mu}_k+\log(\hat{\pi}_k)
\end{equation}\] For QDA, the one feature discriminant function is: \[\begin{equation}
\hat{\delta}_k(x) = x \cdot \frac{\hat{\mu}_k}{\hat{\sigma}_k^2}-\frac{\hat{\mu}_k^2}{2\hat{\sigma}_k^2}+\log(\hat{\pi}_k)
\end{equation}\] Note that \(\hat{\sigma}\) now has a subscript to indicate that the variance is class-specific. For multiple predictors, the QDA discriminant function is again just like the LDA one but with a subscripted \(\Sigma\): \[\begin{equation}
\hat{\delta}_k(x) = x^T\hat{\Sigma}_k^{-1}\hat{\mu}_k-\frac{1}{2}\hat{\mu}_k^T\hat{\Sigma}_k^{-1}\hat{\mu}_k+\log(\hat{\pi}_k)
\end{equation}\] In practice, we will use the lda() and qda() functions that are part of the MASS package in R.
Implementation and Considerations
LDA and QDA both generalize easily to settings where there are more than two classes. They are also parametric, which means they are computationally efficient with large data sets compared to non-parametric KNN. However, they both make the assumption that the features are normally distributed, so you should pay attention to your data. For example, binary variables will never be normally distributed nor well approximated by a normal distribution, and so the methods are not appropriate to use in the presence of binary features.
QDA differs from LDA by assuming the variance or variance-covariance matrix of the feature(s) varies from class to class. This allows for more flexible and non-linear decision boundaries, but requires estimation of more parameters. As with all other models we’ve seen, estimating more parameters increases the likelihood of overfitting and so should only be used when the number of observations is large relative to the number of features and classes.
Coding
The goal of this session is to learn how to implement three classification models: 1. A logistic model 2. LDA 3. QDA
Reminders
To run one line of code in RStudio, you can highlight the code you want to run and hit “Run” at the top of the script. Alternatively, on a mac, you can highlight the code to run and hit Command + Enter. Or on a PC, you can highlight the code to run and hit Ctrl + Enter. If you ever forget how a function works, you can type ? followed immediately (e.g. with no space) by the function name to get the help file
Let’s start by loading the necessary packages and data. We will use the “Default” dataset available from the ISLR package. This dataset contains information on credit card defaults, including a binary response variable “default” and three predictors: “student”, “balance”, and “income”. We will use this dataset to build and evaluate classification models.
Data preparation
Now extract the data and name it “default_data”
default_data <- DefaultLet’s get to know our data
summary(default_data) default student balance income
No :9667 No :7056 Min. : 0.0 Min. : 772
Yes: 333 Yes:2944 1st Qu.: 481.7 1st Qu.:21340
Median : 823.6 Median :34553
Mean : 835.4 Mean :33517
3rd Qu.:1166.3 3rd Qu.:43808
Max. :2654.3 Max. :73554 It looks like we have two categorical variables. We can convert them both to numeric
default_data$default <- as.numeric(default_data$default == "Yes")
default_data$student <- as.numeric(default_data$student == "Yes")Let’s again split our data into test and training data sets with a 20/80 split. We use set.seed() to ensure replicability.
set.seed(222)Then we can use the sample function to split the data (as before)
## First pick the test observations (20% of the data)
test_obs <- sample(seq(nrow(default_data)),
round(0.2 * nrow(default_data)))
## The training observations are the remaining observations
train_obs <- setdiff(seq(nrow(default_data)), test_obs)
## Use the indices now to extract the corresponding subsets of the data
test_data <- default_data[test_obs,]
train_data <- default_data[train_obs,]Logistic regression
Now, let’s say we are interested in using a logistic regression. For a base case, let’s try to predict default from the other available variables using logistic regression. To run logistic regression in R, use glm(), which requires three arguments: - 1st: Your formula (y ~ x1 + x2) - 2nd: Family = binomial tells it to use logistic regression - 3rd: You data, including both x and y columns.
We will train the model on the training data, make predictions for the test data using predict(), and measure performance with Accuracy.
logistic_default <- glm(default ~ student + balance + income,
family = binomial,
data = train_data)To view information about the logistic regression, including coefficients, use summary()
summary(logistic_default)
Call:
glm(formula = default ~ student + balance + income, family = binomial,
data = train_data)
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -1.108e+01 5.654e-01 -19.588 <2e-16 ***
student -5.036e-01 2.638e-01 -1.909 0.0563 .
balance 5.739e-03 2.619e-04 21.916 <2e-16 ***
income 6.727e-06 9.312e-06 0.722 0.4701
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 2320.3 on 7999 degrees of freedom
Residual deviance: 1252.6 on 7996 degrees of freedom
AIC: 1260.6
Number of Fisher Scoring iterations: 8To predict outcomes on the test_data using logistic regression, use:
logistic_predict <-predict(logistic_default,
test_data,
type = "response")
hist(logistic_predict)
# plot auc curves
library(ROCR)
pred <- prediction(logistic_predict, test_data$default)
perf <- performance(pred, "tpr", "fpr")
plot(perf)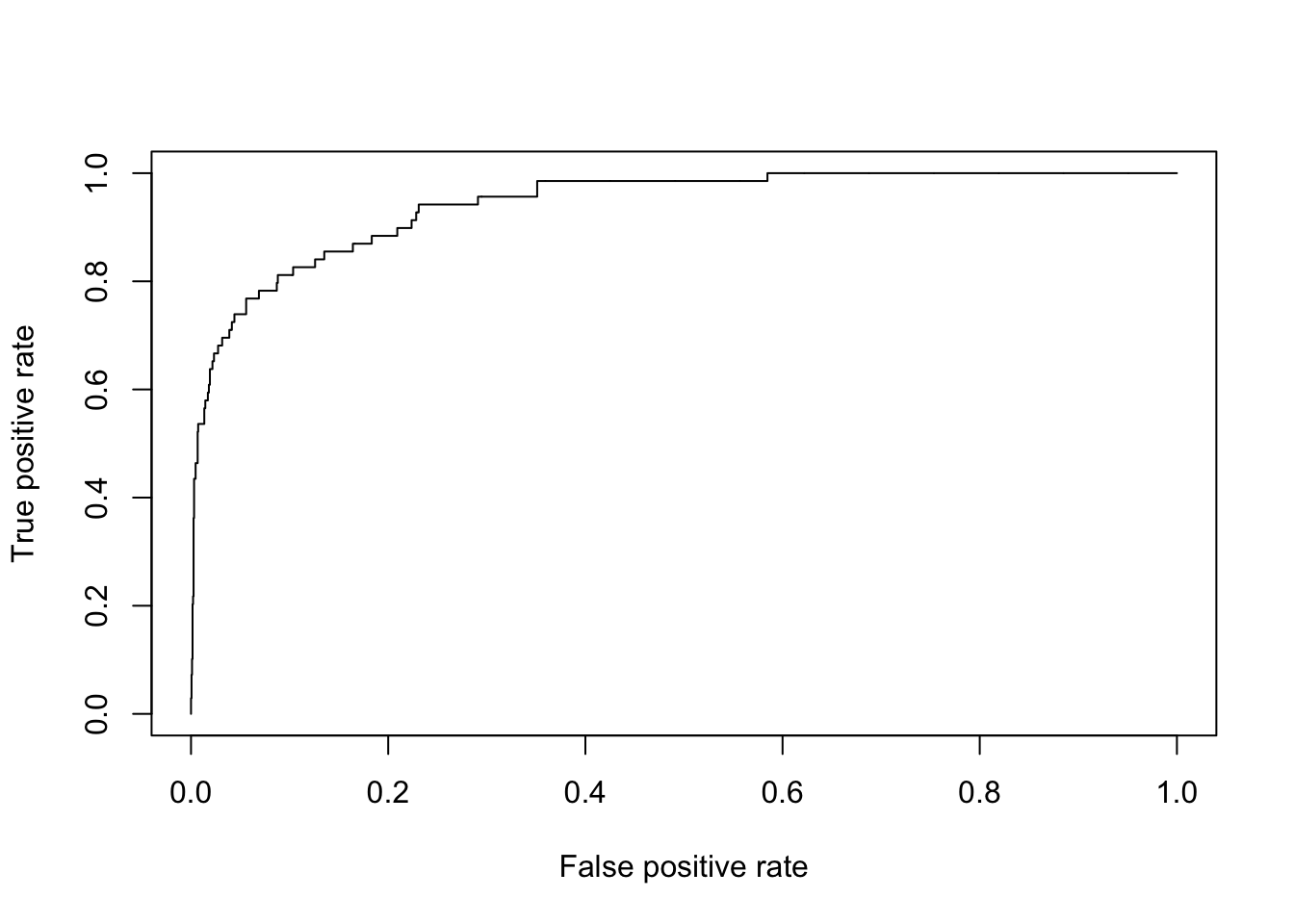
Let’s look at what we got from this prediction model. We will use the head() function, which prints the first few values of the object inside the parentheses. If you want to change the number of observations that are printed to 100, you can use head(object, n = 100)
head(logistic_predict) 4350 18 6678 4788 9481 9994
5.133197e-04 2.176129e-04 2.515555e-03 3.317590e-02 2.508148e-05 4.935658e-03 We see that the prediction outputs are probabilities, so in order to make predictions we have to decide on a decision rule. A common one is if the predicted probability is > 0.5, predict 1 otherwise 0. Let’s see how we would do using this rule. Because it’s a classification problem, accuracy is a good measure (% correct)
class_predictions <- as.numeric(logistic_predict > 0.5)
logistic_accuracy <- mean(class_predictions == test_data$default)
print(logistic_accuracy)[1] 0.9745The accuracy looks great! But, we might care more about different types of errors than overall error rate. For example, we may not want to give loans to people who will default even if this means denying loans to some people who wouldn’t default. We can measure error rate by true default status. Note that for defaulters, default = 1. Here, I pull out all the predictions for the true defaulters and see what fraction of those equal 1.
true_pos_accuracy <- mean(class_predictions[which(test_data$default == 1)] == 1)
print(true_pos_accuracy)[1] 0.3333333Like-wise for the non-defaulters, I see what fraction of those equal 0. This gives class-specific accuracy rates.
true_neg_accuracy <- mean(class_predictions[which(test_data$default == 0)] == 0)
print(true_neg_accuracy)[1] 0.9974107These values summarise what can also be seen in the following table. Where the columns correspond to the true values and the rows correspond to the predicted values.
table(class_predictions, test_data$default)
class_predictions 0 1
0 1926 46
1 5 23Suppose instead of the accuracy, you wanted to directly calculate the error rate. How would you do it? Hint, errors are ones where the prediction does not equal the true value. In R, we use != for “does not equal”
We can also calculate the error rate for the true defaulters and non-defaulters.
true_pos_error <- mean(class_predictions
[which(test_data$default == 1)] != 1)
print(true_pos_error)[1] 0.6666667true_neg_error <- mean(class_predictions
[which(test_data$default == 0)] != 0)
print(true_neg_error)[1] 0.002589332We see that we did a lot better on the true negatives than the true positives. Among all the people who will default, we only predicted about 1/3% of them would default. If we want to do a better job identifying these people, we can do this by lowering the default threshold from a predicted probability of 0.5 to something lower, say 0.2. Note, though, that lowering this threshold means increasing the number of default predictions for people who don’t default as well. Since we aren’t really sure how low we want to make this threshold, we can try for a bunch of threshold values and then see how the performance changes to pick the one that is best for our setting. This involves domain knowledge, such as the cost of default and the earnings on loans extended to people who repay, so there’s not one right answer, but we can more clearly see the tradeoffs by trying many values and plotting the error rates in each group as a function of the threshold.
To do this, we can use a loop to try a bunch of threshold values and then calculate the error rates for each threshold. We can then plot the error rates as a function of the threshold to see how the error rates change as we change the threshold.
## First, we need to specify the list of threshold values to assess
threshold_values <- seq(from = 0.00, to = 0.50, by = 0.01)Then we initialize a matrix of error rates. This matrix will have a number of rows corresponding to the length of the list of threshold values and 2 columns corresponding to the true positive and true negative accuracy for each value that we test
error_rates <- matrix(0, nrow = length(threshold_values), ncol = 2)Now we can start the loop. We initialize a tracker for the row index, then for each threshold value in our specified list of values, we update the tracker to reflect the row, generate the predicted classes using the specific threshold, calculate the true positive accuracy, calculate the true negative accuracy, and add the results to our matrix.
indx <- 0
for(threshold in threshold_values) {
## Update the tracker to reflect the row
indx <- indx + 1
## Then generate the predicted classes using the specific threshold
class_predictions <- as.numeric(logistic_predict > threshold)
## Then calculate the true positive accuracy
true_pos_accuracy <- mean(class_predictions[which(test_data$default == 1)] == 1)
## Then calculate the true negative accuracy
true_neg_accuracy <- mean(class_predictions[which(test_data$default == 0)] == 0)
## Now we can add the results to our matrix
error_rates[indx,] <- c(true_pos_accuracy, true_neg_accuracy)
}
error_rates [,1] [,2]
[1,] 1.0000000 0.0000000
[2,] 0.9420290 0.7560849
[3,] 0.8695652 0.8311756
[4,] 0.8405797 0.8653547
[5,] 0.8260870 0.8886587
[6,] 0.7971014 0.9124806
[7,] 0.7826087 0.9254272
[8,] 0.7681159 0.9347488
[9,] 0.7681159 0.9404454
[10,] 0.7391304 0.9466598
[11,] 0.7391304 0.9523563
[12,] 0.7246377 0.9575350
[13,] 0.7101449 0.9611600
[14,] 0.6956522 0.9627136
[15,] 0.6811594 0.9684102
[16,] 0.6811594 0.9699637
[17,] 0.6811594 0.9715173
[18,] 0.6666667 0.9730709
[19,] 0.6666667 0.9761781
[20,] 0.6521739 0.9782496
[21,] 0.6086957 0.9808389
[22,] 0.6086957 0.9813568
[23,] 0.5942029 0.9823925
[24,] 0.5797101 0.9829104
[25,] 0.5797101 0.9849819
[26,] 0.5652174 0.9860176
[27,] 0.5507246 0.9865355
[28,] 0.5362319 0.9865355
[29,] 0.5362319 0.9886069
[30,] 0.5362319 0.9891248
[31,] 0.5362319 0.9906784
[32,] 0.5362319 0.9917141
[33,] 0.5362319 0.9922320
[34,] 0.5362319 0.9927499
[35,] 0.5217391 0.9927499
[36,] 0.5217391 0.9932677
[37,] 0.5072464 0.9932677
[38,] 0.4927536 0.9932677
[39,] 0.4637681 0.9937856
[40,] 0.4637681 0.9943035
[41,] 0.4492754 0.9953392
[42,] 0.4347826 0.9958571
[43,] 0.4347826 0.9963749
[44,] 0.4347826 0.9963749
[45,] 0.4057971 0.9968928
[46,] 0.4057971 0.9968928
[47,] 0.3768116 0.9968928
[48,] 0.3768116 0.9968928
[49,] 0.3768116 0.9968928
[50,] 0.3623188 0.9974107
[51,] 0.3333333 0.9974107Let’s plot each of these as a function of the threshold
matplot(x = threshold_values,
y = error_rates,
type = "l",
col = 3:4,
xlab = "Threshold",
ylab = "Accuracy",
main = "Accuracy as a Function of Threshold")
legend("topright", legend = c("Defaulters", "Non-defaulters"),
col = 3:4, pch = 1)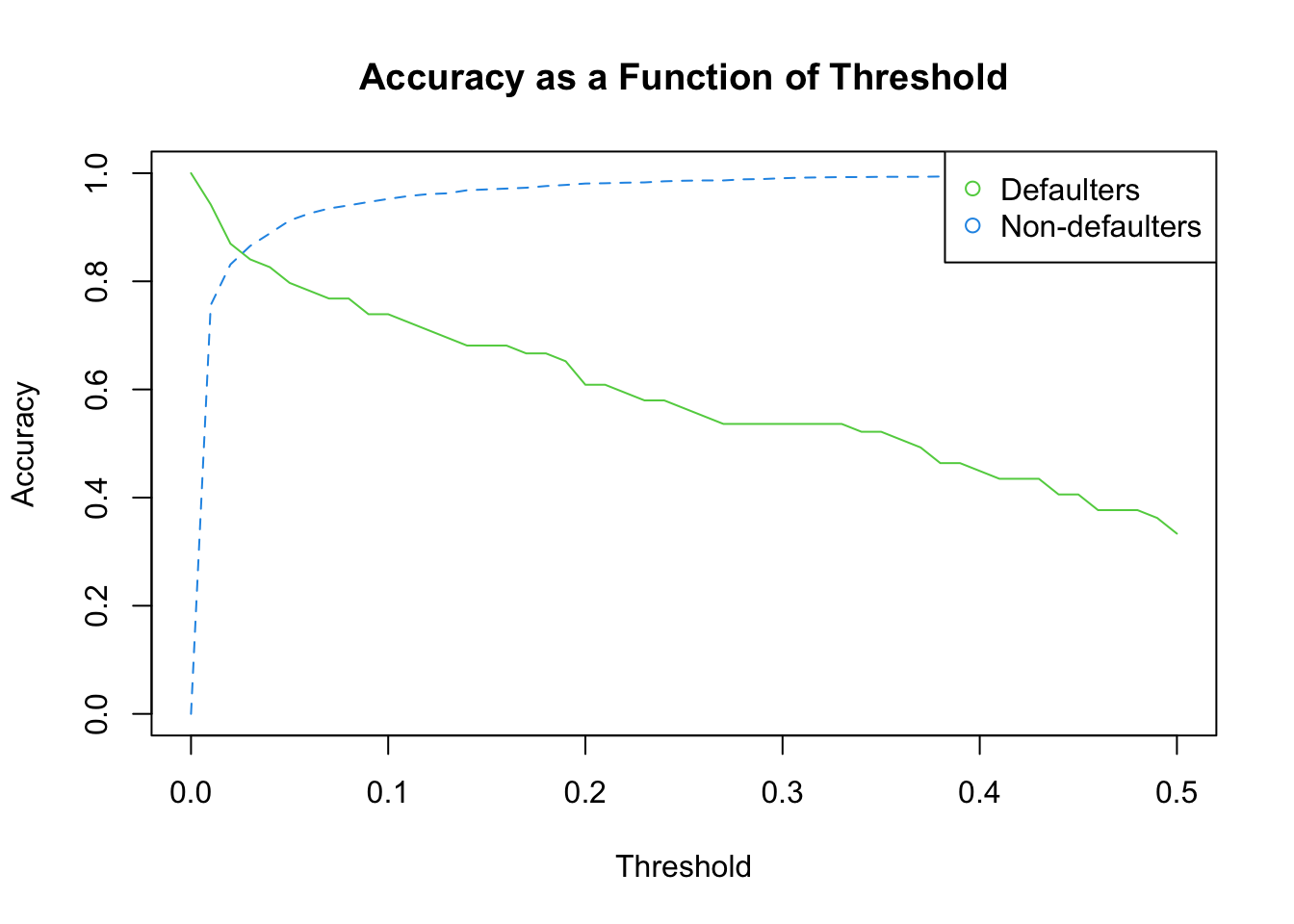
LDAs and QDAs
We can also use other methods to predict default. For example, we can use linear discriminant analysis (LDA) and quadratic discriminant analysis (QDA). These methods are similar to logistic regression, but they make different assumptions about the data. LDA assumes that the data are normally distributed and that the variance is the same in each group. QDA assumes that the data are normally distributed, but it does not assume that the variance is the same in each group.
Note that we need to load the package MASS, because it contains the functions lda() and qda()
library(MASS)Now we can use the “lda” function to run the LDA model.
lda_model <- lda(default ~., data = train_data)We can then generate the predicted values
lda_pred <- predict(lda_model, test_data[,-1])And extract the predicted classes
class_pred_lda <- lda_pred$classFinally, we can calculate the error rate
error_lda <- mean(class_pred_lda !=
test_data$default)
print(error_lda)[1] 0.029To run QDA, we use the “qda” function. Otherwise, the code is the same as with “lda”
qda_model <- qda(default ~., data = train_data)
qda_pred <- predict(qda_model, test_data[,-1])
class_pred_qda <- qda_pred$class
error_qda <- mean(class_pred_qda !=
test_data$default)
print(error_qda)[1] 0.027Summary
In this tutorial, we learned how to use logistic regression, LDA, and QDA to predict default. We also learned how to calculate the error rates for each method. We found that logistic regression had the lowest error rate, but we also saw that the error rates for LDA and QDA were not much higher. This suggests that all three methods are useful for predicting default.